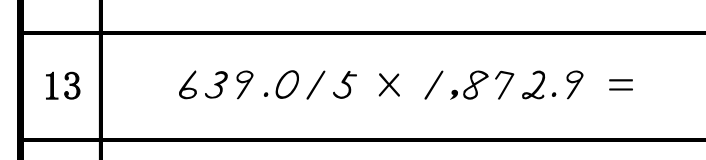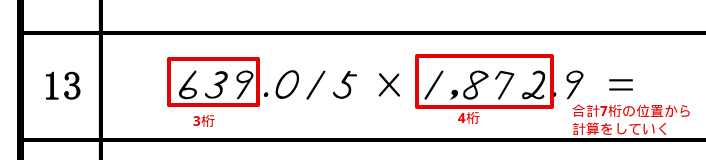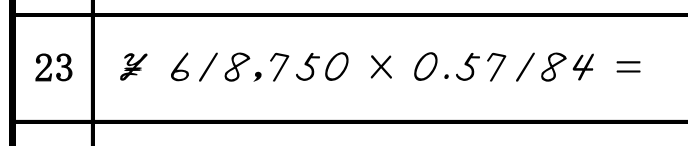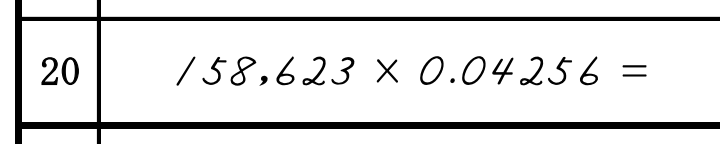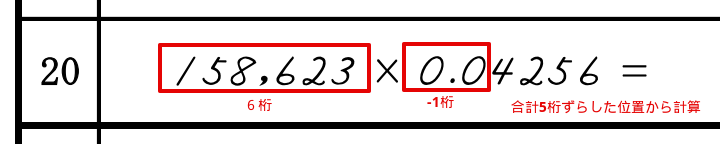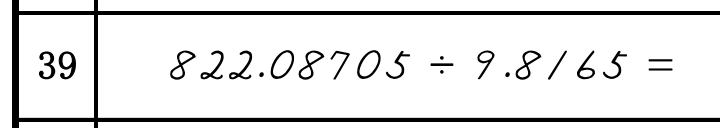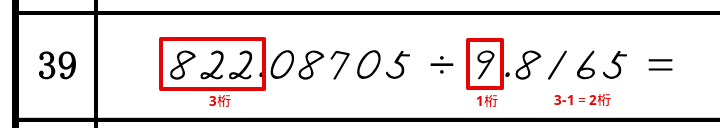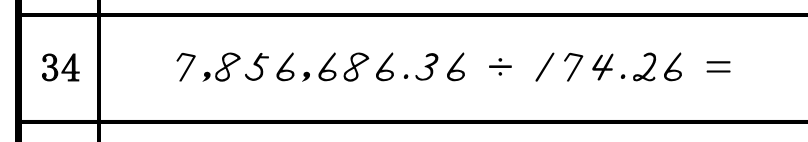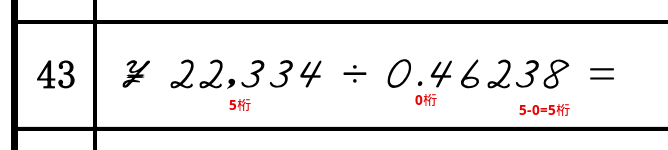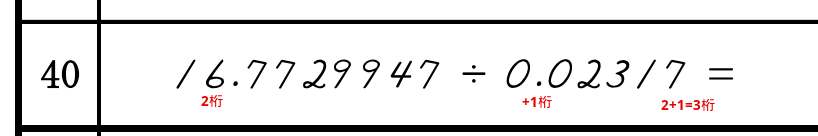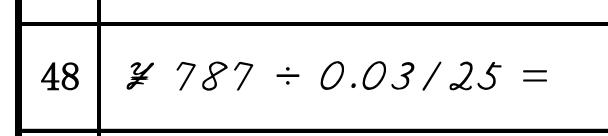そろばんの小数の計算で、小数点の位置の考え方がわからないなぁ...。どうやって決めたらいいんだろう?
本記事では、このような疑問に答えていきます。
本記事の内容
今回は、珠算能力検定試験1級のかけ算、わり算の小数点の位置の決め方について、解説します。
というのも、筆者が最近、中学生のとき以来、そろばんを触ったのですが、小数点の計算をすっかり忘れてしまいました。
そこで今回は、私のやり方をご紹介します。
本記事の信頼性
本記事は、筆者が珠算能力検定試験1級の問題を解いたときの経験に基づいて、執筆しています。
Contents
かけ算の場合
前提
まず、両落としで計算しているものとします。
※両落としとは・・・かけ算を計算する際、かけられる数を置いて計算する方法を片落としと言い、かけられる数を置かずに計算する方法を両落としと言います。
筆者はスピードを上げるため、両落としでやっています。
パターン①:基本的な考え方
かけられる数とかける数の整数部分の桁数を合計し、定位点からその数を移動したところから計算をすればOKです。
こうすると、定位点が小数点の位置になります。
例を見てみましょう。
整数の数を数えます。
この例の場合、3桁と4桁なので、合計7桁を移動した位置から計算していきます。

あとは普通に計算していきます。
定位点の位置が小数点の位置なので、答えは1,196,811.194です。

ほとんどの問題はこれで解けます。
パターン②:0より小さい数の場合(0.x)
0.xの場合は、0桁としてカウントします。
以下の例を見てみましょう。
この場合は6桁+0桁で、6桁移動した位置から計算をしていきます。
パターン③:0より小さい数の場合(0.0x)
0.0xという数の場合は、桁数を-1としてカウントします。
以下の例を見てみましょう。
この場合は6桁-1桁で、5桁移動した位置から計算をしていきます。
わり算の場合
パターン①:基本的な考え方
わられる数の整数部分の桁数から、わる数の整数部分の桁数を引いた数が、答えの整数の桁数になります。
例を見てみましょう。
わられる数が3桁、わる数が1桁なので、3-1で整数部分が2桁とわかります。
これを計算していきます。

整数部分が2桁なので、答えは83.745です。
7割くらいはこれで解けます。
パターン②:わられる数の1番目の数が、わる数の1番目の数より大きい場合
わられる数の1番目の数が、わる数の1番目の数より大きい場合は、桁数を1足す必要があります。
文章だとわかりにくいので、例で示します。
この場合、パターン①のように計算すると、7-3で4桁と求められます。
しかし、わられる数の1番目の数が、わる数の1番目の数よりも大きいので、桁数を+1して、整数は5桁として計算します。
パターン③:0より小さい数がある場合
0.xは0桁として計算します。
0.0xは1桁足してやります。
応用で、以下の問題を考えてみましょう。
パターン②と③の組み合わせで、3桁+1桁+1桁で整数部分が5桁となります。